Spezielle Relativitätstheorie
Einleitung
Was ist Wahrheit? Ist Wahrheit absolut und neutral oder ist sie relativ und kann je nach Betrachter unterschiedlich sein?
Diese Frage begleitet die Menschen durch die Jahrhunderte hindurch und verschiede Kulturen zu verschiedenen Zeiten hatten darauf verschiedene Antworten. Zumindest gab es stets den einen Fixpunkt, auf den sich alle Kulturen verlassen konnten: Zeit und Längen sind in jedem Fall absolut, also für jeden gleich. Wenn Max sagt, dass er eine Stunde gelaufen ist und Peter sagt, er habe nur 59 Minuten gemessen, dann ist entweder einer von beiden richtig oder aber auch keiner. In jedem Fall kann es nicht sein, dass beide mit ihrer Aussage recht haben. Oder doch?
Absolut und relativ
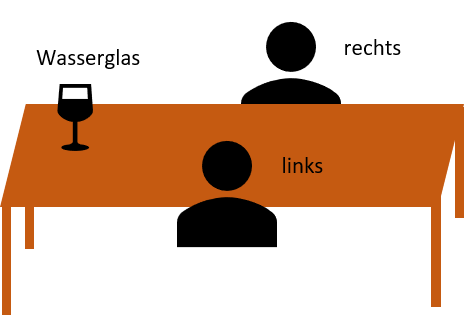
Relativ zum Betrachter bedeutet, dass seine Betrachtungsweise ortsgebunden ist. Ein klassisches Beispiel aus dem Alltag wäre dazu die Ortsangabe mit „links“ und „rechts“. Für den Einen befindet sich das Glas links und für den anderen rechts. Eine absolute Angabe hingegen ist unabhängig vom Betrachter und muss, unabhängig vom Vermesser und der Messmethode, stets dasselbe Ergebnis liefern. So zum Beispiel das Wasserglas, welches auf dem Tisch steht. Ob es ein Glas ist lässt sich durch die Definition eines Glases prüfen und auch der Inhalt kann untersucht werden und wird unabhängig vom Betrachter dasselbe Ergebnis liefern. Auch wenn der eine Beobachter die Tischseite wechselt bleibt es bei demselben Ergebnis: Es ist ein Wasserglas.
Man sagt: „Das Wasserglas steht relativ links/rechts zum Betrachter“
Inertialsystem
Ein Inertialsystem ist ein System, in welchem alle Objekte in derselben gleichförmigen, geradlinigen Bewegung sind. Darunter zählt auch eine konstante Geschwindigkeit von v=0, welche Ruhelage genannt wird.
Angenommen du befindest dich in einem Haus, dann ist dieses Haus, einschließlich dir, ein Inertialsystem. Auch alle Objekte im Haus wie die Tür oder Toaster befinden sich im selben Inertialsystem. Das Inertialsystem befindet sich in Ruhelage, also v=0. Nun siehst du aus dem Fenster einen Zug mit konstanter Geschwindigkeit an dir vorbeifahren. Die Gleise des Zuges hat keine Kurve und somit ist die Bewegung des Zuges sowohl gleichförmig als auch geradlinig. Dieser Zug für sich ist somit wiederum ein Inertialsystem, da alle Objekte des Zuges sich ebenfalls mit der konstanten Geschwindigkeit v bewegen.

Alle Inertialsysteme bewegen sich immer relativ zueinander. Wenn du dich im Haus befindest, dann sind alle Objekte innerhalb diesem relativ zu dir in Ruhelage. Der Zug hingegen bewegt sich mit 100 km/h relativ an dir vorbei. Ein Freund der im Zug sitzt sagt aber, dass er sich in Ruhelage befindet und alles andere, einschließlich dir, mit 100 km/h an ihm vorbeizieht. Diese Aussage ist ebenfalls richtig, da diese Geschwindigkeitsangaben relativ zum Beobachter sind. Was aber absolut ist, ist die Differenz der Geschwindigkeit. Beide Messen jeweils 100 km/h.
Hast du schonmal erlebt, dass du in einem Zug an einem Bahnsteig stehst und dann donnert ein anderer Zug dicht an deinem Fenster vorbei? Wenn du aus dem Fenster schaust, dann wirkt es so, als würdest du fahren und der andere Zug steht. Ist der Zug vorbeigefahren dann siehst du wieder den Bahnsteig und weißt, dass du die ganze Zeit gestanden bist. Falls du das noch nicht erlebt hast probiere das mal! Den Gelehrten Galileo Galilei führte das zu einer verblüffenden Frage: Kann man innerhalb eines Inertialsystems ohne Bezug zur Außenwelt überhaupt feststellen, ob man sich in Bewegung befindet oder nicht?
https://www.youtube.com/watch?v=1Z57k9TVU5k&list=PLtChQtYYwX2PZeFpje0TsiCvXWCpIlBFj&index=3
Das Relativitätsprinzip von Galilei
Dieses besagt, dass es für einen Betrachter innerhalb eines Inertialsystems unmöglich ist, o festzustellen, ob er in Bewegung ist oder nicht. Auch hierfür hilft uns ein Zugbeispiel: Angenommen der Zug fährt auf einem geraden Zug Gleis mit einer konstanten Geschwindigkeit. Zusätzlich hat der Zug keine Fenster. Nun meinte Galilei es sei unmöglich für eine Person im Inertialsystem Zug festzustellen, ob dieser in Bewegung, oder am Bahnhof in Ruhelage ist.
Keine Messung, nicht der Flügelschlag eines Schmetterlings oder die Geschwindigkeit eines fallenden Objekts, könnte Ausschlag über den Bewegungszustandes des Zuges geben. Um dies zu tun bräuchte es einen äußeren Bezugsrahmen.
Einsteins Gedankenexperiment
Zur Zeit Einsteins waren zwei Dinge gewiss: Das Relativitätsprinzip von Galilei (innerhalb eines Inertialsystems, in welchem alle Objekte in derselben gleichförmigen geradlinigen Bewegung sind, ist es unmöglich festzustellen, ob man in Bewegung ist oder ruht.) und das Lichtgeschwindigkeit die schnellstmögliche Geschwindigkeit ist und diese 299 792 458 m/s beträgt. Diese beiden Kenntnisse der Physik bewegten den 16 Jahre alten Einstein zu einem Gedankenexperiment. Auch wenn ein Gedankenexperiment in diesem Sinne kein physikalischer Versuch ist, kann es dennoch physikalische Theorien unterstützen oder wiederlegen.
So stellte sich Einstein vor, wie er mit Lichtgeschwindigkeit mit einem Spiegel in der Hand durchs All düste. Aus dem Alltag wissen wir, dass sich zusammengesetzte Geschwindigkeiten aufaddieren. Angenommen du fährst mit dem Fahrrad 10 m/s und wirfst auf diesem einen Ball in Fahrtrichtung mit 5 km/h, dann addieren sich die beiden Geschwindigkeiten zu 15 km/h. Mit Lichtgeschwindigkeit funktioniert das aber anders, da 299 792 458 m/s der Maximalwert ist. In Einsteins Gedankenexperiment hat er eine Geschwindigkeit von 299 792 458 m/s. Das Licht, welches sein Gesicht reflektiert, bewegt sich ebenfalls mit einer Geschwindigkeit von 299 792 458 m/s. fort.

Würden sich die beiden Geschwindigkeiten aufaddieren, dann würde Licht eine Geschwindigkeit von fast 600 000 000 m/s annehmen was aber nicht geht, da Lichtgeschwindigkeit konstant ist. Die andere Option wäre, dass das Licht Einsteins Gesicht mit Lichtgeschwindigkeit verlässt und dieser das Licht im selben Moment „einholt“. Damit wäre die Geschwindigkeitsdifferenz 0 und die Lichtstrahlen würden nie den Spiegel erreichen. So wüsste Einstein das er in Bewegung ist, was aber dem Relativitätsprinzip von Galilei widerspräche. Welcher dieser beiden Annahmen ist nun also falsch?
Auf diesen Konflikt ist schon der ein oder andere Physiker vor ihm gestoßen, aber Einstein war der erste, der diesen scheinbaren Widerspruch akzeptierte und mit diesem weiter Mathematik betrieb. Oft in der Wissenschaft wurden diejenigen belohnt, die einfach weiterrechneten, auch wenn sich die Ergebnisse ihrer Weltanschauung entgegensetzten.
Die Lösung
Einige werden Einsteins berühmten Satz „Bewegte Uhren drehen langsamer“ kennen. Einsteins Schlussfolgerung aus dem Gedankenexperiment war diese: Ob Einstein sein Spiegelbild sieht oder nicht, ist RELATIV zum Beobachter! Einstein würde sein Spiegelbild ganz normal sehen und er würde nach dem Relativitätsprinzip keine Veränderung wahrnehmen. Gleichzeitig würde ein Beobachter auf der Erde den Einstein vorbeiflitzen sehen, welcher vor einem leeren Spiegel steht.
Auch wenn es höchst unwahrscheinlich klingt schloss Einstein daraus, dass sowohl Zeiten, Längenmaße als auch Masse unterschiedlich sein können, abhängig vom Inertialsystem in dem sich der Beobachter befindet.
Die Mathematik
Wie bereits erwähnt war der Unterschied zu allen anderen Wissenschaftlern, dass Einstein mit diesen Erkenntnissen einfach weiterrechnete. Wir werden in den folgenden Rechnungen die Zeitdilatation herleiten, also dass die Zeit in einem bewegten Inertialsystem langsamer vergeht, aus Sicht eines außenstehenden Betrachters.
Dazu denken wir uns eine Lichtuhr, welche sich in einem Raumschiff befindet. Eine Lichtuhr besteht aus zwei Spiegeln und einem Sensor, welcher die Zeit misst, welche ein Lichtstrahl benötigt, um zwischen den beiden Spiegeln hin und her zu hüpfen. Das Raumschiff befindet sich zunächst in Ruhelage, also die Geschwindigkeitsdifferenz zum Beobachter auf der Erde ist 0. Da sich das Licht innerhalb der Lichtuhr immer mit der konstanten Geschwindigkeit v = 299 792 458 m/s (:=c) bewegt, lässt sich der Weg s (Entfernung Spiegel zu Spiegel) berechnen durch den Zusammenhang s=c*t.


Die direkte Strecke vom Lichtpunkt am untern Spiegel zum Oberen ist c*tErde lang. Die horizontal zurückgelegte Strecke ist v*tErde lang.
Aus Sicht der Rakete hat sich nicht viel verändert unverändert. Die Strecke ist weiterhin c*tRakete lang


Die horizontale Strecke ist die Messung der Rakete mit der Zeit tR für Rakete. Damit ergibt sich für diese Strecke der Zusammenhang sy=c*tR. (sy aufgrund des Weges in Richtung der y-Achse).
Aus Sicht der Erde legt das Licht aber auch einen Weg in x-Richtung mit einer Geschwindigkeit v zurück, abhängig von der Geschwindigkeit der Rakete. So ergibt sich für den Weg in x-Richtung der Zusammenhang sx=v*tE und der resultierende Weg s=c*tE.
Aus dem Alltag würden wir vermuten, dass die Zeiten dieselben sein müssten. Hier aber unterscheiden sie sich voneinander, weshalb wir sie unterschiedlich benennen müssen.
Das Dreieck hat einen rechten Winkel, weshalb wir den Satz von Pythagoras anwenden können. Wir bekommen den Zusammenhang: